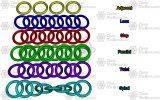
This thread is for the general discussion of the Weave Leanelated. Please add to the discussion here.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I am having a really hard time trying to reduce this to tesselation and cells.
If I am reading this correctly, this is a 4:4 weave, looking very much like its 6:3/3:6 sibling; namely each cell is two large rings, intersected with 2 small rings - and while I say they share a total of 8 small rings, you’ll probably contest me and show how to distribute them to connect to the neighbours.

If I am reading this correctly, this is a 4:4 weave, looking very much like its 6:3/3:6 sibling; namely each cell is two large rings, intersected with 2 small rings - and while I say they share a total of 8 small rings, you’ll probably contest me and show how to distribute them to connect to the neighbours.
Hahahahahahaha, you know ityou’ll probably contest me and show how to distribute them to connect to the neighbours.
well, yes and nonamely each cell is two large rings, intersected with 2 small rings
6 small rings.and while I say they share a total of 8 small rings
There are a few different ways to describe this weave structurally. There are 4 different grain transformations possible with this weave:
-
Leanelated - Lean grain
- Crenelated-3 - Step grain
- Borealis - Parallel grain
- Twistelated - Twist grain (currently undescribed because the correct ARs are still being worked out)
While the above are the base of the weave, to make weave cells, you need at least to of them so you can show the way the cells are connected. I'm going to leave out Twistelated because that has an extra connection that the others do not (which I'm pretty sure changes the base to European 3 in 1). I'm also only going to show building in one direction, it can be done in the opposite direction as well.
These are one of the possible weave cells for the three weaves
From this, we can also figure out the base chains necessary for each of the weaves:
- Leanelated - European 4 in 1 (Dilated Band form)
- Crenelated - Gridlock Sheet (Dilated Band form)
- Borealis - Celtic
Please let me know if you would like further explanation
There are several things that I contest here.
For me, crenelated is a 3:6 weave at the base, and not a 4:4, and borealis is a 3:6 weave at the base. Using subcells, crenelated is 3:6, disregarding subcells as a concept. It’s 6:3.
There’s a huge difference between leanelated and the other two. I am sorry, as I miscounted - it’s of course 10 small rings according to my method, sharing all but 2 (that comes down to 6 rings in total per cell) - but viewing the larger ring as a triangle - leanelated repeats as a pair of triangles forming a parallelogram <> - no smaller shape can be added without changing the pattern, and parallelograms are just distorted squares, making the weave extend with an average of 90 degree rotation
Crenelated can be approximated as 6 triangles, or as with borealis as a hexagon for the smallest repeating (sub)cell, as such, it extends with 60 degrees rotation.
borealis, for me really shows why rings are shared between cells. Each sandwich pair shares 3 sandwiched rings with 3 other sandwich pairs. I know you always try to convince me otherwise, but this cements my view.
For me, crenelated is a 3:6 weave at the base, and not a 4:4, and borealis is a 3:6 weave at the base. Using subcells, crenelated is 3:6, disregarding subcells as a concept. It’s 6:3.
There’s a huge difference between leanelated and the other two. I am sorry, as I miscounted - it’s of course 10 small rings according to my method, sharing all but 2 (that comes down to 6 rings in total per cell) - but viewing the larger ring as a triangle - leanelated repeats as a pair of triangles forming a parallelogram <> - no smaller shape can be added without changing the pattern, and parallelograms are just distorted squares, making the weave extend with an average of 90 degree rotation
Crenelated can be approximated as 6 triangles, or as with borealis as a hexagon for the smallest repeating (sub)cell, as such, it extends with 60 degrees rotation.
borealis, for me really shows why rings are shared between cells. Each sandwich pair shares 3 sandwiched rings with 3 other sandwich pairs. I know you always try to convince me otherwise, but this cements my view.
Forgetting leanelated for a minute, as shown, what would you call the red and green examples in the last render?
Something akin to non-cell incomplete sections of Crenelated and Borealis.Forgetting leanelated for a minute, as shown, what would you call the red and green examples in the last render?
I think you're equating weave cells with segments or units (both of which I haven't posted how they work in CCT). Any weave will need a minimum number of weave cells translated on the appropriate axis before the weave form is recognizable.
are these also incomplete sections?

are these also incomplete sections?
Ah, you meant the very last.
No, those contain all subsegments that will produce the weave.
No, those contain all subsegments that will produce the weave.
Just noticed that you said this:
 )
)
Are you referring to something like this for Crenelated and Borealis?

Because I have some news for you:

 That's the beauty and the horror of chainmaille, there are multiple ways to describe a weave, just as there are multiple ways to assemble weaves. I describe weaves based on CCT (which I will continue to write articles about to try and explain it further).
That's the beauty and the horror of chainmaille, there are multiple ways to describe a weave, just as there are multiple ways to assemble weaves. I describe weaves based on CCT (which I will continue to write articles about to try and explain it further).
In CCT, there is NO rotation between weave cells, ONLY translations (except in spiral grains, but grains are an entirely different aspect that will be discussed in yet another articlerepeating (sub)cell, as such, it extends with 60 degrees rotation.
Are you referring to something like this for Crenelated and Borealis?
Because I have some news for you:
For you (and everyone else), any weave can be whatever you wantFor me, crenelated is a 3:6 weave at the base, and not a 4:4, and borealis is a 3:6 weave at the base. Using subcells, crenelated is 3:6, disregarding subcells as a concept. It’s 6:3.
In CCT, the ONLY difference between these three weaves are the grains that the large rings form:There’s a huge difference between leanelated and the other two.
Then CCT is noway near enough, I'm sorry. Leanelated introduces an element that really changes the topology. The topology for crenelated can be reduced to the single ring with 6 small rings working as a triangle. The topology for borealis requires what you posted. As you see for both of them, you can rotate them 120 degrees and you'll be where you started. With Leanelated, you won't, you need a 180 degree rotation (and a flip). If you rotate borealis 180 degrees, you do not have the same edge towards you, you need to rotate 60 degrees in either direction and a flip won't change that.Just noticed that you said this:
In CCT, there is NO rotation between weave cells, ONLY translations (except in spiral grains, but grains are an entirely different aspect that will be discussed in yet another article)
Are you referring to something like this for Crenelated and Borealis?
View attachment 8711
Because I have some news for you:
View attachment 8712
For you (and everyone else), any weave can be whatever you wantThat's the beauty and the horror of chainmaille, there are multiple ways to describe a weave, just as there are multiple ways to assemble weaves. I describe weaves based on CCT (which I will continue to write articles about to try and explain it further).
In CCT, the ONLY difference between these three weaves are the grains that the large rings form:
- View attachment 8713 Leanelated is a Lean grain \\\\\\\\
- Crenelated is Step grain _-_-_-
- Borealis is Parallel grain -=-=-=
Then CCT is noway near enough for me, I'm sorry.Then CCT is noway near enough, I'm sorry.
Fixed that for you.
You are comparing apples and oranges.
Using CCT, by simply changing where the base cells are connected I can show how you can go from a Leanelated unit to a Crenelated unit and from a Crenelated unit to a Borealis unit by modifying it with the addition of the extra adjacent layer and an increase in AR of the smaller rings to allow for that extra layer. This is just 2 out of the 3 cells needed to create units of each weave.
- If the light blue ring in leanelated under the dark blue ring, it would be Crenelated.
- If I put the orange ring over the red ring in Crenelated, it would be Leanelated.
- If I put another red and orange under the first and third rings AND parallel with the second and fourth, (or over the second and fourth and parallel with the first and third) in Crenelated, it would be Borealis.
- If I took away the bottom large rings OR the top large rings in Borealis, it would be Crenelated.
and what? You're comparing a segment of Leanelated sheet to a unit of Crenelated and a unit of Borealis. With Crenelated and Borealis sheets, the segments are the same as the units, with leanelated they are not. Please note, I am talking based on CCT definitions. If I make a unit (as per CCT, because that's how I do things) what you state above is incorrect.As you see for both of them, you can rotate them 120 degrees and you'll be where you started. With Leanelated, you won't, you need a 180 degree rotation (and a flip). If you rotate borealis 180 degrees, you do not have the same edge towards you, you need to rotate 60 degrees in either direction and a flip won't change that.
Top Row - Left side is a segment of Leanelated sheet, right side is a unit of Leanelated
Bottom Row - Left side is a segment of Leanelated sheet rotated 120 degrees on a central axis, right side is a unit of Leanelated rotated 120 degrees on a central axis:
The right side, from what I can see, cannot extend to a sheet as leanelated.Then CCT is noway near enough for me, I'm sorry.
Fixed that for you.As I've said multiple times CCT is a different way of looking at things and it may not be everyone's cup of tea.
You are comparing apples and oranges.
Using CCT, by simply changing where the base cells are connected I can show how you can go from a Leanelated unit to a Crenelated unit and from a Crenelated unit to a Borealis unit by modifying it with the addition of the extra adjacent layer and an increase in AR of the smaller rings to allow for that extra layer. This is just 2 out of the 3 cells needed to create units of each weave.
- If the light blue ring in leanelated under the dark blue ring, it would be Crenelated.
- If I put the orange ring over the red ring in Crenelated, it would be Leanelated.
- If I put another red and orange under the first and third rings AND parallel with the second and fourth, (or over the second and fourth and parallel with the first and third) in Crenelated, it would be Borealis.
- If I took away the bottom large rings OR the top large rings in Borealis, it would be Crenelated.
View attachment 8717
and what? You're comparing a segment of Leanelated sheet to a unit of Crenelated and a unit of Borealis. With Crenelated and Borealis sheets, the segments are the same as the units, with leanelated they are not. Please note, I am talking based on CCT definitions. If I make a unit (as per CCT, because that's how I do things) what you state above is incorrect.
Top Row - Left side is a segment of Leanelated sheet, right side is a unit of Leanelated
Bottom Row - Left side is a segment of Leanelated sheet rotated 120 degrees on a central axis, right side is a unit of Leanelated rotated 120 degrees on a central axis:
View attachment 8725
the left side - does extend to a sheet, but as you demonstrate, You can clearly see that it's rotated, and can realign it. You can't with The other two. That's what makes it a 4:4 and not a 3:6 or 6:3.
Correct, because the right side is a unit of Leanelated. CCT does not use units to make sheets (although they can be modified to become weave cells which can then be translated into weave forms).The right side, from what I can see, cannot extend to a sheet as leanelated.
What do 4:4 and 6:3 have to do with CCT? CCT deals with translations, You're talking about:the left side - does extend to a sheet, but as you demonstrate, You can clearly see that it's rotated, and can realign it. You can't with The other two. That's what makes it a 4:4 and not a 3:6 or 6:3.
- Taking a segment of a sheet form
- Rotating it 120 degrees
- Making new cells that are now going against the grain instead of with it. Of course it's not going to work the way you're trying to do it!!! It completely changes the connections between the cells. Look at the large green and azure in relation to the large blue and red rings in the left and right examples below. They are not the same. Lean grain is directional and continuous, while step and parallel grains are alternating. That's why you can rotate them and they work, your way.
When looked at with CCT, the sheet forms of all 3 (4 counting Twistelated) weaves are made with transformations of the same weave cell. The difference is how the weave cells are connected to each other.
Which is why when extended and expanded through CCT, the one on the right does work:
Last edited:
Similar threads
- Replies
- 0
- Views
- 394
- Replies
- 0
- Views
- 331
- Replies
- 2
- Views
- 505
- Replies
- 1
- Views
- 434
- Replies
- 0
- Views
- 301