The Dual Grain Persian Revision
Periodically, in Biology, as new discoveries and new information are uncovered over time, taxonomic revisions are made. I see no reason why a similar "structural revision" could not be applied to chainmaille. Much like its biologic counterpart, this structural revision will focus on identifying and structurally naming all the weaves within that group, determining their relationships to each other, and classifying them according to their shared characteristics.
Naming Note: I have no interest (in most cases) of trying to change any of the "commonly accepted" names of these weaves. As such, on this site at least, I will be introducing a field for "Structural Names". In cases of there being no current commonly accepted name for a weave, the structural name will be used.
The main subject of this revision will be, what I currently call, Dual Grain Persians. It will only include the base forms and not any modified versions. For the purpose of this revision, Dual Grain Persians will be examined as a Spinal Grain (parallel to X surface) and an Inverted Lock Grain. (perpendicular to X surface). Dual Grain Persians are made up of, as you might have already guessed, two grains. In cases where the same grain is used for both the Spinal and Inverted Lock grains, that weave will be designated as the "base weave" for that subgroup. Dual Grain Persians are commonly referred to as Half Persian 3 in 1 weaves.
Future Research: It's my belief that the concepts presented here can also be applied to, (at the very least) other "Persian" weaves such as Paired Grain Persian (already done), Three Quarters Persian, and Hilt. I have made some preliminary steps in said research, but more needs to be done before anything can be published.
This revision is largely possible due to the tireless work of Dave Austin (_CMB_), proprietor/collator of chainmailbasket.com, the most prolific listing of weaves on the internet. Without our conversations and his work into Full Persian 6 Cross Grains, this revision would not exist.
Naming Note: I have no interest (in most cases) of trying to change any of the "commonly accepted" names of these weaves. As such, on this site at least, I will be introducing a field for "Structural Names". In cases of there being no current commonly accepted name for a weave, the structural name will be used.
The main subject of this revision will be, what I currently call, Dual Grain Persians. It will only include the base forms and not any modified versions. For the purpose of this revision, Dual Grain Persians will be examined as a Spinal Grain (parallel to X surface) and an Inverted Lock Grain. (perpendicular to X surface). Dual Grain Persians are made up of, as you might have already guessed, two grains. In cases where the same grain is used for both the Spinal and Inverted Lock grains, that weave will be designated as the "base weave" for that subgroup. Dual Grain Persians are commonly referred to as Half Persian 3 in 1 weaves.
Future Research: It's my belief that the concepts presented here can also be applied to, (at the very least) other "Persian" weaves such as Paired Grain Persian (already done), Three Quarters Persian, and Hilt. I have made some preliminary steps in said research, but more needs to be done before anything can be published.
This revision is largely possible due to the tireless work of Dave Austin (_CMB_), proprietor/collator of chainmailbasket.com, the most prolific listing of weaves on the internet. Without our conversations and his work into Full Persian 6 Cross Grains, this revision would not exist.
What is an Inverted Lock Connection?
An inverted lock connection is one of the four, currently recognized, connections in Cellular Chainmaille Theory. For the purpose of explaining how CCT differentiates connections, each ring will be shown in 2 halves (A/B or C/D).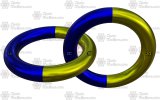 This is a Root Cell. Root Cells are made up of two rings (when unmodified in any way). Ring 2C connects to Ring 1B.
This is a Root Cell. Root Cells are made up of two rings (when unmodified in any way). Ring 2C connects to Ring 1B. This is a direct connection between two root cells. Cell Two (3A) connects to Cell One (2D).
This is a direct connection between two root cells. Cell Two (3A) connects to Cell One (2D). This is an inverted connection between two root cells. Cell Two (3A) connects to Cell One (2C).
This is an inverted connection between two root cells. Cell Two (3A) connects to Cell One (2C). This is an inverted lock connection between two root cells. Cell Two (3A) connects to Cell One (2C) AND Cell Two 4D is rotated and "locked" into place inside Cell One - Ring 1.
This is an inverted lock connection between two root cells. Cell Two (3A) connects to Cell One (2C) AND Cell Two 4D is rotated and "locked" into place inside Cell One - Ring 1.Weaving Note: When extending a chain, each extension (XA) will connect to the previous cell (XC) AND (XD) rotated and "locked" in place inside the previous cell - Ring X.
What Are Grains?
Filling In the Blanks
Commonly accepted names will be in parenthesis. Cells link to the associated Maillepedia entry. "Redundant" entries are marked as such because they have already been named elsewhere in the table. There are a total of 15 different dual grain persians.| Spine > IL V | Lean | Step | Parallel | Twist | Spiral |
| Lean | Lean Persian (Half Persian 3 in 1) | Redundant | Redundant | Redundant | Redundant |
| Step | Lean Persian - Step (Kirsti) | Step Persian (Half Persian 3 in 1 (Alternating)) | Redundant | Redundant | Redundant |
| Parallel | Lean Persian - Parallel (Half Persian Split) | Step Persian - Parallel | Parallel Persian (One and a Half Persian) | Redundant | Redundant |
| Twist | Lean Persian - Twist (Half Persian 3 in 1 (Interlock)) | Step Persian - Twist | Parallel Persian - Twist | Twist Persian (Japanese Rain Chain) | Redundant |
| Spiral | Lean Persian - Spiral (Half Persian Spiral) | Step Persian - Spiral | Parallel Persian - Spiral | Twist Persian - Spiral | Spiral Persian (Japanese Rain Chain (Spiral)) |
What's The Point?
As I asked myself many times while I was doing this, you may have also asked yourself "What's the point?" The main reason is that Dual Grain Persians are the chains that progress into 3 or 4 grain Persians. Much like the "Full Persian" name in regards to Paired Grain Persians, you'll see Half Persian used all over the place with some exceptions. If one, or more, of them are worthy of different names, because they are different weaves, then shouldn't all of them be worthy of different names? By revising these Dual Grain Persians we get consistency of naming as well as consistency in what makes them different from each other. In addition, by providing a solid base, we are able to track which weave can be considered a base for further progressions (3 grain persians, paired grain persians, etc.) as well as how they are progressed.
The below sub groups are shown in order of seniority. You will notice that there are less entries in each group as you go down the list. What this means is that as you move through the chart, you will come across weaves that have already been given names based on a senior grain present in the weave.
Grain Note: You may have noticed that the Dual Grain Persians utilize Parallel as a single grain. This is due to Parallel being a progression of adjacent and step. Just like them, if you do not add a "cross grain" it's just a pretty pile of rings with no connections. It is also senior to twist due to the lack of connections.
Render Note: While the following renders have physics applied, the final positions of the rings in our reality may have different "final" positions depending on the alignment of the weave and how it is displayed (free hanging or on a surface). Regardless of final positions, the structure remains the same.
The below sub groups are shown in order of seniority. You will notice that there are less entries in each group as you go down the list. What this means is that as you move through the chart, you will come across weaves that have already been given names based on a senior grain present in the weave.
Grain Note: You may have noticed that the Dual Grain Persians utilize Parallel as a single grain. This is due to Parallel being a progression of adjacent and step. Just like them, if you do not add a "cross grain" it's just a pretty pile of rings with no connections. It is also senior to twist due to the lack of connections.
Render Note: While the following renders have physics applied, the final positions of the rings in our reality may have different "final" positions depending on the alignment of the weave and how it is displayed (free hanging or on a surface). Regardless of final positions, the structure remains the same.
Lean
Lean Grain is primary because it results in the first of the Inverted Lock chains (Half Persian 3 in 1)
Defining Grain: Lean
Base Weave: Lean Persian (Half Persian 3 in 1)
Number of Weaves: 5
Redundant Weaves: 0
Descendant Groups: Mirror Lean Persians, Layered Lean Persians
Step
Step grains are next because it is an alternating version of Lean grain.
Defining Grain: Step
Base Weave: Step Persian (Half Persian 3 in 1 (Alternating))
Number of Weaves: 4
Redundant Weaves: 1
Descendant Groups: Mirror Step Persians, Layered Step Persians
Parallel
Parallel grain is a layered progression of Step grain.
Defining Grain: Parallel
Base Weave: Parallel Persian (One and a Half Persian)
Number of Weaves: 3
Redundant Weaves: 2
Twist
Twist is the next grain because it is actually two joined adjacent grains.
Defining Grain: Twist
Base Weave: Twist Persian (Japanese Rain Chain)
Number of Weaves: 2
Redundant Weaves: 3
Descendant Groups: Mirror Twist Persians, Layered Twist Persians
Spiral
Spiral is the last grain because it is a further modification of twist grain.
Defining Grain: Spiral
Base Weave: Spiral Persian (Japanese Rain Chain (Spiral))
Number of Weaves: 1
Redundant Weaves: 4
Descendant Groups: Layered Spiral Persian
Additional notes: Rotations, Chirality, and Alternate Versions
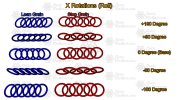
 All Dual Grain Persian weaves are one continuous spinal grain and one continuous inverted lock grain. One of these grains will always be an X Rotation (Roll). As we are focusing on dual grain persians, these rotations really have no effect on which weave you are making (e.g. two lean grains, regardless of their rotation, will always be Half Persian 3 in 1 (Lean Persian)). However, while the degree of x rotation has no effect on which dual grain persian weave you are making, it may have an effect on how your completed weave looks
All Dual Grain Persian weaves are one continuous spinal grain and one continuous inverted lock grain. One of these grains will always be an X Rotation (Roll). As we are focusing on dual grain persians, these rotations really have no effect on which weave you are making (e.g. two lean grains, regardless of their rotation, will always be Half Persian 3 in 1 (Lean Persian)). However, while the degree of x rotation has no effect on which dual grain persian weave you are making, it may have an effect on how your completed weave looksThis is especially true of lean and step grains. Looking at the below graphic, you can see that while a +/- 180 degree X rotation gives the same result, a +/- 90 degree X rotation gives mirrored results. Parallel and Twist grains get mirrored results through offsetting of their sequence (i.e. Parallel starting with 2 rings instead of 1 or the second twist ring being a negative X rotation from the first instead of a positive X rotation.) Spiral grains will always be mirrored through a counterspiral.
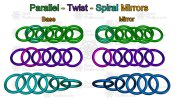
 It is this mirroring that can give you a different looking final result and remain the same weave (e.g. Half Persian 3 in 1 - Left vs. Right). In mathematics (and chainmaille) this is known as Chirality (sometimes called "Handedness"). If a weave cannot, through rotations and/or translations, overlap its mirror image it is said to be Chiral. While single grains (other than spiral) are achiral (not chiral), when joined together as a dual grain persian, the resulting weave may be chiral.
It is this mirroring that can give you a different looking final result and remain the same weave (e.g. Half Persian 3 in 1 - Left vs. Right). In mathematics (and chainmaille) this is known as Chirality (sometimes called "Handedness"). If a weave cannot, through rotations and/or translations, overlap its mirror image it is said to be Chiral. While single grains (other than spiral) are achiral (not chiral), when joined together as a dual grain persian, the resulting weave may be chiral.
